June 11th, 2018
Randomly Selecting Points within a Given Polygon
References Used:
Stack Overflow – Random Points in a QuadrilateralWolfram Alpha Information on Points in a Triangle
Notes
I needed to be able to randomly but evenly distribute a number of objects within a 2D area so these are the sources I started with. The Stack Overflow question ended up being a very good starting point, but there were errors with the calculations that I needed to solve in order to actually use their logic.
Fixes from Stack Overflow
First calculation to fix was the originally randomly selected position of the object. It turned out that it was very close, but it actually only worked if v0 was the origin. It was simple enough to fix by adding v0 to the x equation.
The second equation to fix was the v3 equation. They were subtracting v0 twice which is incorrect (again something unnoticeable if v0 is that origin as you’re simply subtracting (0,0) twice). v0 should only be subtracted once to obtain the correct v3 value.
Finally, a correction that was found in the comments was that there are two rotation equations for x’ and the larger one is incorrect. In the text, it can be found that a rotation of pi is necessary. This can be mathematically applied by simply reversing (x – v3) to (v3 – x).
Work to do
Fixing these mathematical errors has appeared to give me the desired results with some further testing required after a final issue. I still need to determine how to let it know mathematically when to “flip” the x position into the x’ position. The original thought was to simply compare the distance from x to v3 and v0, and if it was closer to v3 (distance was less), then apply the x’ flip transformation. This however does not seem to be a geometrically sound solution as I am sometimes getting the flipped applied when it is within the proper bounds.
July 2nd, 2018
Update: Resolved issue for determining when to flip the spawn positions
Reference:
Point in Triangle Test: Math Foundation
Building off of the previous work and calculations being done, the points for the triangles to contain the objects to spawn already exist. Using these with the calculations found in the reference for “Point in Triangle Test”, it can be determined if the point the collectible will be spawned at is indeed within the 3 vector locations of the vertices of the triangle. If it is not, then the “flip” algorithm is applied to put it into the triangle.
The test uses the existing triangle to basically check the cross products of each edge with the potential spawn location and the location of the third/final vertex of the triangle. As long as the directions of the cross product results of these two checks are the same, it can be concluded that the points are on the same side of the tested edge. If this is applied to all three edges, and the case is true for all three, it can be concluded that the point is within the triangle. If any of these are false, it is outside of the triangle and the “flip” algorithm is applied.
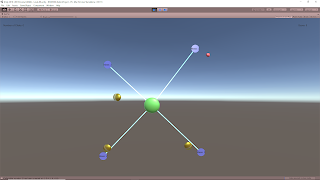Video of Spawner in Action
This shows a few test runs of having the collectibles randomly spawned to check if they consistently spawn within the play area. The small red orbs that sometimes appear are error checking markers added to help determine if everything was working properly. These are spawned right before an out of bounds collectible if flipped, to leave an indication of where it was at to see if it was truly out of bounds. Some of them appear very close to the edges of the play area, but those still appear to be just outside of the triangle and seem to be getting flipped into the play area effectively so those seem correct as well.
